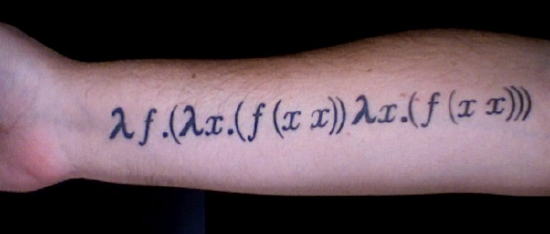I've done a fair bit of coding in Haskell, yet I could never fully understand monads. And if you don't get monads then coding Haskell is... tense. I could still get things done with some amount of cargo culting, so I was able to use them, but I couldn't understand what they really were.
I tried several times to figure it out, but all the explanations seemed to suck. People are so excited by the universality of monads that they make up all kinds of esoteric metaphors and the more of them you hear about the less you understand. Meanwhile there's no simple explanation to be found. That's when they're not simply too eager to skip ahead to equations that have them weeping like an art critic in front of the Mona Lisa and tell you all about the monadic laws as it that helps.
Fortunately, help is at hand, for today I will show you the first truly good explanation of monads I've ever seen, written by the charming Dan Piponi in the distant 2006 (I rather wish I had found it sooner). What I will do here is use Dan's method to explain it, using some python examples for easier comprehension, and keep it even more basic.
Rationale
![]() It's good to get this one straightened out right off the bat. Basically, it's nice to be able to have some piece of data that you can pass to any number of functions, however many times you want, and in whatever order you want. Imagine them lined up one after another like a pipeline, and your data goes through it. In other words: function composition. We like that because it makes for clear and concise code.
It's good to get this one straightened out right off the bat. Basically, it's nice to be able to have some piece of data that you can pass to any number of functions, however many times you want, and in whatever order you want. Imagine them lined up one after another like a pipeline, and your data goes through it. In other words: function composition. We like that because it makes for clear and concise code.
To achieve this we need functions that can be composed, ie. have the same signature:
def inc(x):
return x+1
def double(x):
return x*2
print "Primitive funcs:", double( inc(1) )
# Primitive funcs: 4
Logging functions
![]() Sometimes, however, you find that you want to add something to a function that is not strictly necessary to participate in the pipeline. Something that is more like metadata. What if you wanted your functions to also log that they had been called?
Sometimes, however, you find that you want to add something to a function that is not strictly necessary to participate in the pipeline. Something that is more like metadata. What if you wanted your functions to also log that they had been called?
def inc_log(x):
return inc(x), "inc_log called."
def double_log(x):
return double(x), "double_log called."
# This will not work properly:
print "Logging funcs:", double_log( inc_log(1) )
# Logging funcs: ((2, 'inc_log called.', 2, 'inc_log called.'), 'double_log called.')
# What we wanted:
# Logging funcs: (4, 'inc_log called.double_log called.')
Now, instead of each function taking one input and giving one output, it gives two outputs. So what happened when we ran it was this:
inc_logreceived1inc_logreturned(2, 'inc_log called.')double_logreceived(2, 'inc_log called.')double_logreturned((2, 'inc_log called.', 2, 'inc_log called.'), 'double_log called.')Instead of doubling the number it doubled the tuple.
Restoring composability (bind)
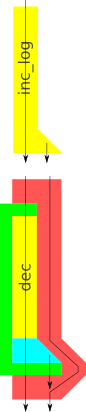
 So how can we solve this? It's not that hard. If you look at the diagram you see that
So how can we solve this? It's not that hard. If you look at the diagram you see that inc_log produces two outputs, yet double_log should only receive one of these. The other should still be saved, somehow, and then joined with the output of double_log after it's finished executing. So we need a wrapper around double_log to change the arguments it receives and change the arguments it returns!
def bind(g):
def new_g(pair):
f_num, f_str = pair
g_num, g_str = g(f_num)
return g_num, f_str + g_str
return new_g
new_double_log = bind(double_log)
print "Logging funcs:", new_double_log( inc_log(1) )
# Logging funcs: (4, 'inc_log called.double_log called.')
The name "bind" is not the most self explanatory imaginable, but what the wrapper does is just what we said in the description:
- Receive a pair of values.
- Call
double_logwith the first of these values. - Receive a new pair of values from
double_log. - Return a third pair of values that we construct from the other pairs.
The key thing to notice is this: we have "adapted" double_log to be a function that accepts two inputs and returns two outputs. We could use the wrapper on any number of other functions with the same "shape" as double_log and chain them all together this way, even though their inputs don't match their outputs!
Mixing function types
 So far so good, but what if we now we want to mix logging functions with primitive functions in our pipeline?
So far so good, but what if we now we want to mix logging functions with primitive functions in our pipeline?
def dec(x):
return x-1
# This will not work:
new_dec = bind(dec)
print "Logging funcs:", new_dec( inc_log(1) )
Granted dec is not a logging function, so we can't expect it to do any logging. Still, it would be nice if we could use it without the logging.
But we can't use bind with dec, because bind expects a function with two outputs. dec simply does not have have the shape of a logging functions, so we are back to square one. Unless...
Using bind with primitive functions
Unless we could fake it, that is. And make dec look like a logging function. In the diagram we can see that there is a gap between the end point of dec and that of bind. bind is expecting two outputs from dec, but it only receives one. What if we could plug that gap with a function that lets the first output through and just makes up a second one?
def unit(x):
return x, ""
 Yes, just like that! Except that now we have two functions
Yes, just like that! Except that now we have two functions dec and unit, and we don't want to think of them as such, because we really just care about dec. So let's wrap them up so that they look like one!
def lift(func):
return lambda x: unit( func(x) )
lifted_dec = lift(dec)
new_dec = bind(lifted_dec)
print "Logging funcs:", new_dec( inc_log(1) )
# Logging funcs: (1, 'inc_log called.')
So lift does nothing more than calling dec first, then passing the output to unit and that's it. dec+unit now has the shape of a logging function and lift wraps around them both, making the whole thing into a single function.
And with the lifted dec (a logging function should anyone inquire), we use bind as we've done with logging functions before. And it all works out!
The log says that we've only called inc_log. And yet dec has done its magic too, as we see from the output value.
Conclusions
If you look back at the diagram you might think we've gone to a lot of trouble just to call dec, quite a lot of overhead! But that's also the strength of this technique, namely that we don't have to rewrite functions like dec in order to use them in cases we hadn't anticipated. We can let dec do what it's meant for and do the needed plumbing independently.
If you look back at the code and diagrams you should see one other thing: if we change the shape of logging functions there are two functions we need to update: bind and unit. These two know how many outputs we're dealing with, whereas lift is blissfully ignorant of that.

 March 11th, 2012
March 11th, 2012